Project Name: Why Flow-Completion Time is the Right Metric for Congestion Control
Team Members: Lisa Yan (yanlisa@stanford.edu) and Richard Hsu (richardhsu@stanford.edu)
Goals: What problem was the original paper trying to solve?
Congestion control algorithms often focus on maximizing throughput, link utilization, and fairness, which are goals catering more towards operators than users of the network. In the early 2000s, Internet traffic primarily consisted of webpage requests or reading emails: small data requests that users wanted to complete as quickly as possible. However, since congestion control algorithms like those found in vanilla TCP cater to longer flows like downloading files, VoIP, etc., many flows lasted longer than necessary. Thus users at the time were seeking shortest flow completion time (FCT).
Motivation: Why is the problem important/interesting?
This problem is important because previous algorithms favored the long-lived flows whereas much of the Internet traffic consists of short-lived flows. This problem is important to look at so that algorithms are better designed for the user experience as users expect faster FCTs rather than maximized throughput, link utilization, and fairness.
Results: What did the original authors find?
The original authors created and implemented Rate Control Protocol (RCP) to address the problem and focus on what users really wanted which is the shortest FCT. This protocol attempts to model processor sharing and from tests run gives a good approximation for processor sharing. RCP shows significant improvement in FCTs for various flow sizes as compared to TCP and Explicit Control Protocol (XCP) which has been proposed as well as a better congestion control protocol over TCP.
Subset Goal: What subset of results did you choose to reproduce?
We chose to reproduce the subset of results that compare the average FCT and max FCT for various flow sizes for RCP, TCP, XCP as well as slow-start and processor sharing (PS), which is an optimal that all congestion protocols try to approximate. This is Figure 12 in the full “Why Flow-Completion Time is the Right metric for Congestion Control and why this means we need new algorithms” paper (http://yuba.stanford.edu/techreports/TR05-HPNG-112102.pdf).
Subset Motivation: Why that particular choice?
Figure 12 shows the most immediate impact of the results. It shows that for the FCT metric, the author’s protocol RCP works closer to the optimal of PS, whereas TCP and XCP perform consistently worse for short flows. This result makes the RCP protocol a worthwhile improvement of perceived quality, or FCT, for the majority of the customers that drive the economics of the Internet.
Subset Results: How well do the results match up? Explanation if you see significant differences.
From the RCP website (http://yuba.stanford.edu/rcp/), the authors provided support code for RCP for the network simulator, ns-2, and simulation examples for running TCP, RCP, and XCP with stated Poisson arrivals and Pareto flow length distribution. We ran the provided TCP and RCP simulations and followed the website’s equations to produce output for Slow-Start and Processor Sharing (PS); however we were not able to run XCP as will be discussed in the Challenges section.
The following are our results compared to the results of the paper. The experiment was to simulate a single link with capacity 2.4 Gbps and RTT 100 ms; flows arrive according to a Poisson distribution with rate parameter lambda, (rho = 0.9, where the load rho is the ratio of lambda to service rate; service rate is the number of flows served per second, i.e. capacity/(average flow size)), and the packet length of each flow is distributed according to a Pareto distribution of shape 1.2 and mean of 25 packets.
 |
 |
 |
 |
| Our Results | Paper Results (Figure 12) |
As you can see our results are comparable with the results presented in the RCP paper. The most noticeable difference is that in our simulation runs, RCP results have a slightly longer average flow completion time (roughly 0.1s) for small flows and do not follow Processor Sharing as well as in the RCP paper. We noticed in the simulation scripts provided that the mean packet size was calculated based off the bandwidth-delay product, which, with the values given by the paper, would yield a mean packet size of 30 rather than 25 as stated in the figure caption. We instead decided to use the original assumptions given by the caption and set the mean packet size to 25. The Poisson arrival parameter, lambda, is dependent on this value which differs by around 2000, which we at first believed could make a significant difference in the number of flows acting in the system which could end up changing the results; however, we tested this hypothesis by changing the parameters back to the original values but the results were similar and the difference was still present. Other than this, we do not believe there are any other differences besides using NS-2.35 instead of NS-2.30 and cannot explain the slight difference, though the results maintain the same trend.
As for the max flow completion time, the results seem to be on par with those given in the paper:
 |
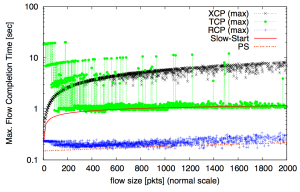 |
| Our Results | Paper Results (Figure 12) |
Challenges: What challenges did you face in implementation?
The RCP authors provided code for their implementation and some simulation examples on their website. However, it was implemented for NS-2.30 which has issues being compiled under newer versions of GCC and running on newer operating systems. Consequently we modified NS-2.35 to work with the RCP code since NS-2.35 can compile under more recent operating systems such as Ubuntu 14.04. We’ve included a patch file with our code for the required modifications of NS-2.35 files and inclusion of actual RCP protocol files to run the simulations.
We were not able to get the XCP simulation working and were not able to determine the cause of why the simulation would not process. NS-2 uses OTCL which we are unfamiliar with, so extending the original example code and fixing issues such as with XCP became too time consuming for this project. After spending many hours on the issue, we decided that the real importance of this article was going to be comparing RCP with TCP so we made sure to get these simulations working.
Critique: Critique on the main thesis that you decided to explore – does the thesis hold well, has it outdated, does it depend on specific assumptions not elucidated in the original paper?
The Rate Control Protocol is a really good implementation that shows improved performance in flow completion time – which is what users want – over general TCP and XCP – which aim for high throughput. However, the RCP results are not necessarily what network administrators want in their network. They want high throughput and link utilization which means they are more likely to not implement the router configurations necessary for users to take advantage of RCP. Also RCP was only designed in an academic environment with no real world tests, therefore less likely to be implemented in commercial environments. However, this could be more useful in a more closed network such as data centers. This lends to the design of Data Center TCP (DCTCP) in that respect which actually references the RCP paper “Processor sharing flows in the Internet” (N. Dukkipati, M. Kobayashi, R. Zhang-Shen, and N. McKeown. In IWQOS, 2006.).
Extensions: Any exploration outside the results in the paper?
(a) Pareto Distribution Exploration
We were curious about the Pareto distribution used for the flow size distribution and read more about it. The Pareto distribution is a heavy tailed distribution with two parameters: shape and mean. Typical networks will see a large range of flow sizes, where the majority of them of them are small. We’ve seen typical traffic flow size models to follow a Pareto distribution with a shape between 1 and 2. Any shape below 2 will yield an infinite variance (and below 1 yields an infinite mean); therefore typical models have a large range of flows but still maintain the heavy tailed property. We wanted to see how TCP and RCP would act in a heavy tailed distribution but with a finite variance; thus we tested the simulations with Pareto distributed flow sizes with shape of 2.2 instead of 1.2. This may be more typical for networks with many small flows and only a few flows that are medium-sized, such as environments with general web browsing traffic and occasional, reasonably-sized file downloads.
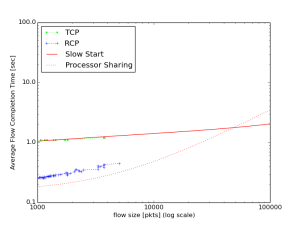 |
 |
 |
As you can see from these graphs, RCP still outperforms TCP and still approximates PS well, whereas TCP is closer to slow-start. This is because there were not very large flows present in the network; therefore most flows could achieve higher rates and therefore complete quickly. Also as you can see by inspection that all flows are below 10,000 packets which with 1,000 bytes each packet would yield roughly 10 Mb files. Therefore in a system with just small flows, RCP will still outpace TCP as the “algorithm makes flows last much longer than necessary” (Dukkipati). Thus we believe this was an interesting extension as it helped us better understand the overall picture of not just a generalized setting and confirm that even with only small flows acting in the network that TCP will still make flows last much longer than necessary.
(b) Processor Sharing (Custom Simulations)
We have not studied queueing theory in depth and thus we wanted to analyze processor sharing more deeply than the formula used in the paper to generate the graphs. The formula used was in http://yuba.stanford.edu/~nanditad/RCP-IWQoS.pdf (L is the flow size, C is the capacity and, rho is the load of the network):
This is more of a lower bound that does not depend on the simulation of traffic flows; the average RTT increases as 1/(1-rho) from queueing theory. We therefore decided to implement our own PS simulation with similar assumptions on the Poisson arrival rate and Pareto distribution of flow sizes. Our Python simulation used the SciPy library to generate the simulated arrivals and flow length distribution; we computed the optimal link allocation with processor sharing and compared them to the paper’s processor sharing equation. In parallel, we also decided to write another PS simulation that used the RCP simulation’s log file data to calculate the optimal link allocation on the same set of traffic flows. The following are the results of these two custom PS simulations:
 |
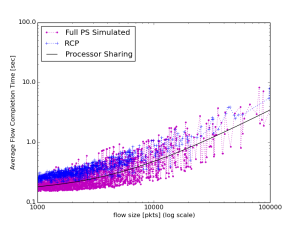 |
 |
| Full PS Simulation (SciPy Library) | ||
 |
 |
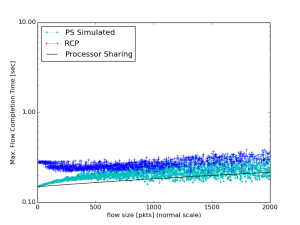 |
| PS Simulation (Using RCP Data) | ||
As you can see our simulated data, both custom PS simulations yield data that follows the formulaic PS algorithm used by the paper. This gave us more confidence in the equation as well without having to derive it. Note that since it is a simulation, the values do not exactly the line; however, the general trend should be evident.
Platform: Choice of your platform, why that particular choice and how reproducible is the entire setup, what parameters of the setup you think will affect the reproducibility the most?
We chose to use Ubuntu 14.04 LTS operating system for reproducing the work. The reason for this is that the original authors had simulation code for NS-2 which works fairly well with the Ubuntu Operating System. That being said, we also used NS-2 since the provided code was made to work with NS-2. For our given modifications, reproducibility should be straightforward as installing NS-2, downloading our version of the simulation code, and running it. This can be easily done on a personal system or on Amazon’s EC2 service.
README: Instructions on setting up and running the experiment.
You can find an image for reproducing the results on Amazon EC2. In the Oregon center, we have a community AMI called “CS244-2014-RCP” that has the reproduction environment already set up. Once the image has started, go into the folder cs244-14-rcp/simulation/ and type ./run.sh; the graph results should appear in the cs244-14-rcp/simulation/graphs/ folder! Note that the simulations and plotting will take roughly 1.5 hours to complete; you should use screen or tmux so that any server or network disconnection issues do not interrupt the run.
See the README for https://github.com/richardhsu/cs244-14-rcp if you want to attempt to set up the reproduction environment on your own system.
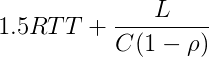
Score for reproducibility: 5
Comments on sensitivity analysis: The results in the report are very interesting because the flow completion times for short flows are much smaller compared to TCP flows whereas flow completion times for large flows is comparable to that of TCP. I would have expected contention between number of short flows and completion times for long flows. This is because if RCP was able to perfectly mimic processor sharing, flow completion times of long flows do not suffer much. However if you constantly prefer short flows, then the flow completion time of long flows suffer. There is sensitivity analysis in the report relating to this. It considers two kinds of distributions of traffic – one presented in the paper and other with large number of short flows. So, from the results in the report, even with large number of small flows, RCP performs well. However, the figure does not indicate the presence of any long flows at all for Pareto distributed flow sizes with shape of 2.2. I understand that the flows of smaller sizes are more likely but not having a single flow of large size prohibits us from making any conclusions about the effect on flow completion times of large flows because of RCP.
Comments on reproducibility: With the information presented in the report, one can create a topology and traffic on another platform like Mininet too. So I believe that experiment can be reproduced with the given information.